Negative Harmony Calculator
Input the key, then input the chord you'd like translated to it's negative form.
Tonic
♮/♯/♭
Modality
Chord
Negative Harmony
undefined
What is negative harmony?
Recently popularized by Jacob Collier, negative harmony is a theory that suggests that translating a chord across a tonic/dominant axis will produce another chord with the same potential function due to its intervallic structure in relation to the tonic.

Although it's easier to visualize as a midway point between the tonic and dominant, the axis that we're translating across is at E-quarter-flat. If we take each chord tone and replace it with it counterpart across this axis, we'll generate our negative harmony. For example, A minor's negative counterpart is E-flat major. How would you figure this out without using the calculator 🤔? By translating each of the chord's tones across the axis:
- A would be converted to B-flat
- C would be converted to G
- E would be converted to E-flat
If we follow the same procedure for all diatonic chords, we can make a chart that should be true for all keys 😲:
- I turns into i
- ii turns into ♭VII
- iii turns into ♭VI
- IV turns into v
- V turns into iv
- vi turns into ♭III
- vii° turns into ii°
Coincidentally, the chart above also covers the minor scale. Notice how the translations from right to left procude the chords of the natural minor scale. In the case of melodic minor, the chart accounts for ii and vii°, but not vi° and III+, because they require a chromatic alteration that isn't included in the parallel major.
- vi° turns into iii°
- ♭III+ turns into ♭VI+
You can also use these shortcuts if you want to calculate negative harmonies on the fly:
- To get the scale degree of the negative harmony, subtract your starting scale degree from 9. I.e 2 turns into 7 because 9 minus 2 is equal to 7.
- Major chords become minor, and vice versa.
- Diminished and augmented chords keep their quality.
With all that being said, you should be able to trust the chart, or the quick and dirty method, above for every key; however let's test it in the key of F major and see if the translations are correct.
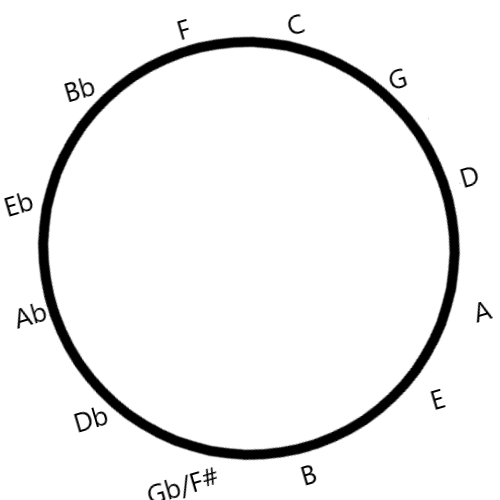
Because we found the negative harmony for A minor in relation to C major in the first example, let's try D minor here. As we hypothesized above, vi's negative counterpart should be ♭III.
- D would be converted to E-flat
- F would be converted to C
- A would be converted to A-flat
Ernst Levy 👨🏫 is the theorist credited with discovering this and detailing his approach in his textbook Theory of Harmony. However, after reading the book myself, although Levy goes into detail about concepts such as polarity and telluric gravity, I couldn't find a reference to this specific approach, which involves taking the circle of fifths and rotating it to create an imaginary axis between E-flat and E-natural.
Instead, on page 25 for instance, we see that C remains the axis, and that G translates to F, E to A-flat, etc. . Levy does comment on the idea of the label subdominant being a fallacy due to both dominant and subdominant behaving similarly. But other than this, I can't seem to find a passage that suggests this exact method, despite it being the consensus method across the web 🌐.
In fact, I never saw the term negative harmony used once; however, I think it is a fantastic way to illustrate the harmonic relationships being theorized here. 🎵